Wiele, jeśli nie większość reakcji przeprowadzanych przez chemików, ale i tych, które zachodzą w przyrodzie ożywionej, zachodzi w roztworach. Najpopularniejszym rozpuszczalnikiem, a więc i środowiskiem reakcji jest woda. Rozpuszczone w niej kwasy, zasady i sole ulegają reakcji dysocjacji elektrolitycznej i występują w postaci jonów, otoczonych cząsteczkami wody (czyli hydratowanych).
Większość reakcji kwasów nie zależy od anionów reszty kwasowej, ale zależy od obecnych w ich roztworach jonów (kationów) wodorowych, H+, a ściślej - "uwodnionych" jonów hydroksoniowych (hydronowych - jony wodorowe chętnie łączą się z cząsteczkami wody, wiązaniem koordynacyjnym), H3O+. W większości przypadków roważanych w szkole średniej wystarczy stosować uproszczony zapis H+.
Można więc powiedzieć, że odczyn kwaśny, to taki stan roztworu wodnego, w którym, w roztworze, są obecne jony wodorowe. Jest to jednak stwierdzenie bardzo "jakościowe" - ściślej, należałoby podać wartość stężenia molowego jonów H+, oznaczanego najczęściej symbolem [H+]. Analogicznie zdefiniować można odczyn zasadowy, jako taki stan roztworu, w którym obecne są w nim jony OH-, a ściślej, podając ich stężenie, [OH-] w roztworach wodorotlenków, czy - szerzej - zasad.
Można by więc przypuszczać, że roztwór obojętny, to roztwór wodny, który nie zawiera ani jonów wodorowych, ani wodorotlenowych. Tyle, że taki roztwór wodny ... nie istnieje. Okazuje się bowiem, że woda ulega w niewielkim stopniu samorzutnej dysocjacji (tzw. autodysocjacji) na jony:
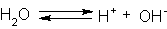, a ściślej: 
.
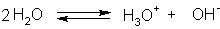Co więcej, z tzw. prawa działania mas wynika, że dla reakcji autodysocjacji wody obowiązuje stała równowagi, która w tym przypadku przyjmuje postać tzw. iloczynu jonowego wody:
Wartość ta jest zwykle podawana bezwymiarowo, o ile wartości stężeń molowych, oznaczonych tu nawiasem kwadratowym, są wyrażone w molach na decymetr sześcienny. Wartość podana dotyczy temperatury ok. 20°C, w temperaturach znacznie niższych lub wyższych jest ona odpowiednio mniejsza lub większa.
Konsekwencją prawa działania mas jest obecność w każdym roztworze wodnym zarówno jonów H+, jak i OH-, przy czym ich stężenia muszą zawsze spełniać warunek zapisany iloczynem jonowym wody. W szczególności, łatwo zauważyć, że w "czystej" wodzie, ale również w innych, rozcieńczonych roztworach obojętnych,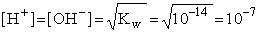 
, co wyrażone jest w mol/dm3.
Wynika z powyższego wniosek, że wszystkie roztwory kwasów zawierają więcej niż 10-7M jonów wodorowych. Rozważmy kilka przykładów.
Analogicznie, jeżeli stężenie HCl wynosi, np., 10-3M, to stężenie jonów H+ wynosi 10-3M, a gdy stężenie HCl wynosi 10-5M, to [H+] = 10-5M. Niestety, gdy stężenie kwasu osiąga warość rzędu 10-6M lub mniejszą, okazuje się, że nie można już pominąć obecności w roztworze jonów wodorowych pochodzących z autodysocjacji wody!
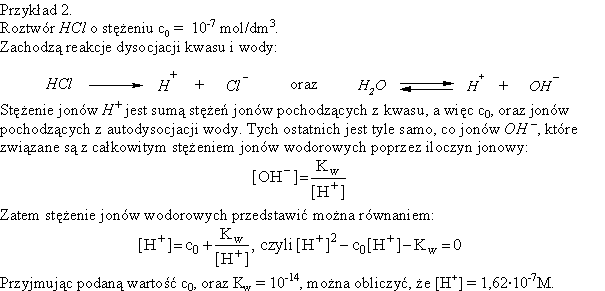
Nieco bardziej skomplikowane obliczenia są konieczne, aby określić stężenie jonów wodorowych w roztworach słabych kwasów.
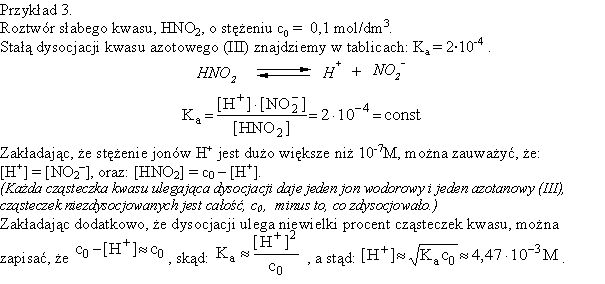
Warto zauważyć, że uzyskany wynik spełnia przyjęte założenia. O ile jest dość oczywiste, że 4,5·10-3 jest dużo większe od 10-7, to mniej jasne jest stwierdzenie, że wynik jest dużo mniejszy od 0,1. Chemicy przyjmują zwykle w takiej sytuacji, że "dużo mniejsze" oznacza "ponad dwadzieścia razy mniejsze" - a taka zależność jest tu spełniona (choć "ledwo - ledwo").
W tym miejscu można już zauważyć, że stężenie jonów wodorowych wyraża się zwykle liczbami z zakresu od 10-7 do ok. 10-1, no może 100 = 1 mola/dm3. Co prawda, stężone roztwory kwasów mogą zawierać jeszcze więcej jonów wodorowych, ale w takich roztworach nie można już pomijać udziału wody w reakcji dysocjacji, nie można też założyć stałego stężenia "wody w wodzie", co wyklucza używanie stałej dysocjacji wody w uproszczonej posatci iloczynu jonowego.
Analogiczne obliczenia dla roztworów mocnych i słabych zasad prowadzą do takiego samego stężeń jonów wodorotlenowych. Zauważyć jednak można, że zamiast stężenia jonów OH-, dla określania zasadowości roztworu można używać również stężenia jonów H+ - przecież [H+] = Kw/[OH-]. Zatem wartościom [OH-] z zakresu
10-7 do 10-1 odpowiadają wartości [H+] od 10-7 do 10-13, a dla [OH-] = 1M, [H+] = 10-14M.
W 1909 roku, duński chemik S.P.L. SØrensen (1868 - 1939) zaproponował uproszczony sposób zapisywania stężenia jonów wodorowych. Zamiast podawać liczbę w postaci 10-xM, wystarczy podać sam wykładnik potęgi, i to bez minusa. Tak zapisaną symbolicznie wartość [H+] określa się jako pH roztworu. Zatem:
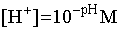
Analogicznie zdefiniować można "wykładnikowy" zapis innych stężeń, np. pOH, czy wartości stałych równowagi, pK. W szczególności, ponieważ Kw = 10-14, zapisać można pKw = 14. Ponieważ mnożeniu potęg odpowiada dodawanie wykładników, łatwo zauważyć, że wyrażenie na iloczyn jonowy wody, czyli:
Kw = [H+]·[OH-] = 10-14, odpowiada zapis "wykładnikowy":
pH + pOH = pKw = 14
log10 x = y , gdy x = 10y. Często stosuje się uproszczony zapis: lg x.
Przykłady: lg 1 = 0, bo 100 = 1; lg 1000 = 3, lg 0,0001 = -4 itp.
Skalę logarytmiczną, a więc zapis logarytmów zamiast liczb, stosuje się wszędzie tam, gdzie wartości mierzone różnią się o wiele rzędów wielkości.
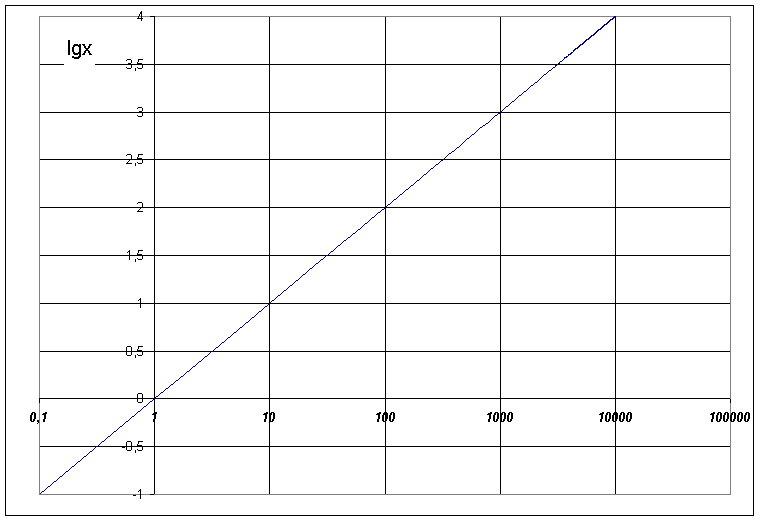
Aby obliczyć wartość pH, gdy stężenie jonów H+ wynosi np. 4,5·10-3, jak w przykładzie 3., trzeba skorzystać z kalkulatora wielodziałaniowego, tablic matematycznych lub odpowiedniego wykresu.
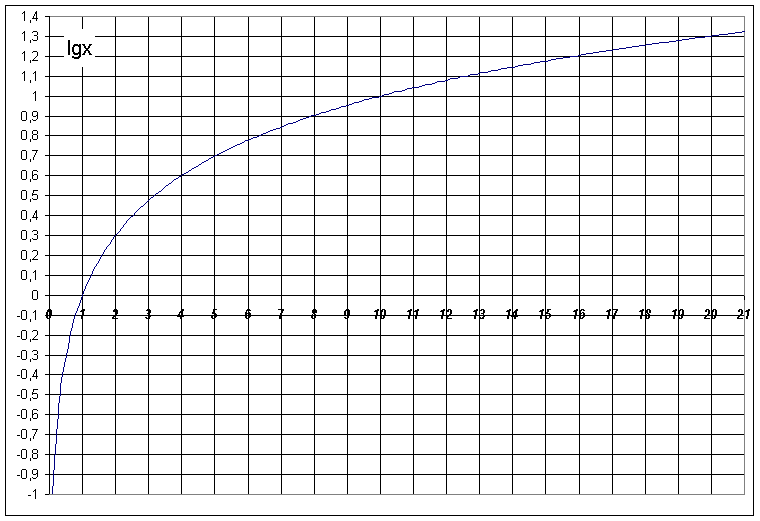
Pamiętać przy tym trzeba o zależności:
lg (x·y) = lg x + lg y.
Zatem, gdy [H+] = 4,5·10-3, pH = - lg [H+]/1M = - (lg 4,5 + lg 10-3)
pH = - (0,65 - 3) = 2,35 (wartość logarytmu liczby 4,5 odczytać można z wykresu).
Skala pH znalazła powszechne zastosowanie w chemii. Jej znajomość jest potrzebna każdemu, kto ma do czynienia nie tylko z chemią ale i biologią, rolnictwem techniką, medycyną itd. Podsumowując można zapisać poznane wyżej wzory:
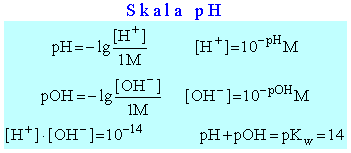
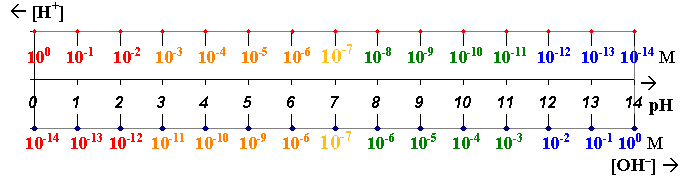
Po wprowadzeniu definicji pH wróćmy do pojęcia odczynu roztworu. Skoro w roztworach kwasów obecne są jony H+, w stężeniach większych niż w samej wodzie, czyli większych od 10-7M, to pH roztworów kwaśnych jest mniejsze od 7. W roztworach obojętnych i w czystej wodzie pH wynosi 7, natomiast roztwory zasadowe, w których dominują jony OH-, a jonów wodorowych jest w nich mniej niż 10-7M, posiadają pH większe od 7.
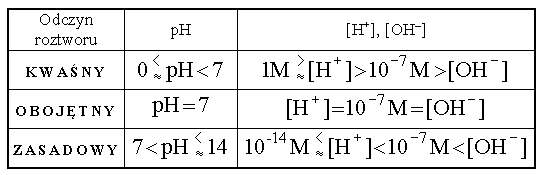
<--- odczyn kwaśny |
obojętny |
odczyn zasadowy ---> |
|||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
W przykładach rachunkowych przytoczonych wyżej i w ananlogicznych przykładach roztworów zasadowych, pH przyjmuje następujące wartości:
| Roztwór | Stężenie jonów H+ | pH |
| HCl, c0 = 0,1M | [H+] = 10-1M | 1 |
| HNO2, c0 = 0,1M | [H+] = 4,5·10-3M | 2,35 |
| HCl, c0 = 0,001M | [H+] = 10-1M | 3 |
| HCl, c0 = 10-7M | [H+] = 1,6·10-7M | 6,80 |
| NaOH, c0 = 10-7M | [OH-] = 1,6·10-7M [H+] = 6,2·10-8M | 7,21 |
| NaOH, c0 = 10-3M | [OH-] = 10-3M [H+] = 10-11M | 11 |
| NaOH, c0 = 0,1M | [OH-] = 10-1M [H+] = 10-13M | 13 |
Opracował: MW 2008, na podstawie materiałów własnych
