W pierwszej połowie XIX w. rozwinęła się teoria atomistyczna. Około roku 1860, nie bez oporów, zaczęto stosować powszechnie pojęcia atomu i cząsteczki, w takim znaczeniu, jakie dziś poznajemy zaczynając naukę chemii w gimnazjum. Tak więc atom traktujemy jako najmniejeszą cząstkę pierwiastka chemicznego, a cząsteczkę, jako zbudowaną z atomów, najmniejszą cząstkę związku chemicznego.
Przeprowadzając reakcje chemiczne w warunkach umożliwiających pomiary masy lub objętości reagentów, zauważono, że substancje wchodzące w reakcję lub w niej powstające pozostają w stałych stosunkach masowych (gazy - również objętościowych). Jest to odzwierciedleniem atomowej budowy materii - cząsteczka powstając z atomów zachowuje stosunek mas tych atomów. Na podstawie pomiarów tego typu ustalono, że najlżejszym atomem jest atom wodoru. Masy innych atomów i cząsteczek zaczęto wyrażać jako wielokrotności masy tego atomu. Z przyczyn, można powiedzieć, natury technicznej, za jednostkę masy atomowej uznaje się obecnie 1/12 masy atomu węgla, izotopu 12C, ale jej sens pozostaje taki sam - jest to, w przybliżeniu, masa najlżejszego atomu.
Tak więc, masa atomowa, to masa atomu danego pierwiastka, wyrażona w jednostkach masy atomowej, a masa cząsteczkowa - masa cząsteczki danego związku, wyrażona w jednostkach masy atomowej (pomijając w tym miejscu kwestie izotopów, średnich ważonych itp.). Jednostkę masy atomowej można oznaczać, jako "u", choć wolę skrót "j. m. at." - odpowiednik amerykańskiej "amu" - "atomic mass unit".
Z prawa zachowania masy wynika, że ilości reagentów w reakcji chemicznej są proporcjonalne do ich mas atomowych i/lub cząsteczkowych, z uwzględnieniem liczby atomów / cząsteczek biorących udział w reakcji.
Masy atomowe znajdziemy w każdym układzie okresowym, podane zwykle do kilku miejsc po przecinku. W praktyce, najczęściej, wystarczy odczytywać masy atomowe z dokładnością do liczb całkowitych, może z wyjątkiem chloru, dla którego przyjęcie masy atomowej 35,5 j. m. at. jest obarczone błędem poniżej 1%, w przeciwieństwie do wartości "35". Dla przykładu: masy atomowe wodoru i tlenu, to, odpowiednio, 1 j. m. at. i 16 j. m. at.; masy cząsteczkowe wodoru, tlenu i wody - odpowiednio - 2 j. m. at, 32 j. m. at. oraz 18 j. m. at.
Rozważmy prosty przykład:
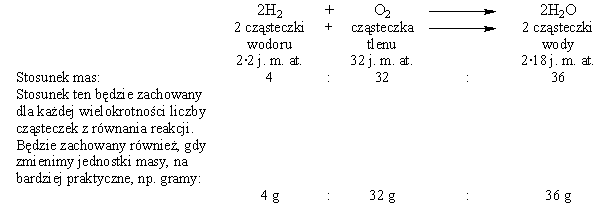
Tak więc, w tradycyjnym znaczeniu, mol, to ilość substancji, której masa wyrażona w gramach jest liczbowo równa masie atomowej lub cząsteczkowej.
Równanie reakcji z przykładu zinterpretujemy zatem:
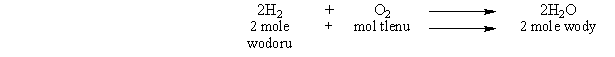
Pozostaje jednak pytanie, jaki jest ten współczynnik proporcjonalności, który pozwala na przejście od jednostek masy atomowej do gramów - ile jednostek "mieści się" w jednym gramie? Otóż jest to tzw. liczba Avogadro, której nazwa pochodzi od nazwiska włoskiego uczonego z XIX wieku, Amadeo Avogadro. Liczba ta wynosi, w przybliżeniu:
Współczesna definicja mola odnosi się właśnie do liczby Avogadro: Mol to ilość materii, która zawiera liczbę Avogadro cząstek (atomów, cząsteczek, jonów itp). Definicja mola w układzie SI brzmi może trochę bardziej zawile, ale sprowadza się do przytoczonej.
Pojęcie mola pozwala odnieść ilość substancji, wyrażoną w dowolny sposób, do mola tej substancji. Dotyczy to masy, liczby cząstek oraz objętości. Okazuje się przy tym że, dla gazów, objętość jednego mola, mierzona w danych warunkach, jest praktycznie niezależna od rodzaju gazu. W tzw. warunkach normalnych (0°C, czyli 273K, 1 atm, czyli 101325 Pa), mol dowolnego gazu zajmuje objętość ok. 22,4 dm3. Zależności pomiędzy masą, objętością i liczbą cząstek, a ilością substancji wyrażoną w molach (tzw. liczbą moli) przedstawia schemat, którego idea pochodzi z artykułu Bernarda S. Browna, A Mole Mnemonic, Journal of Chemical Education Vol. 68, N°12, December 1991:
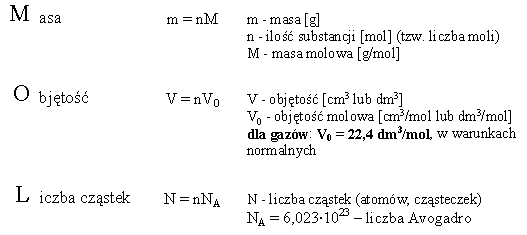
|
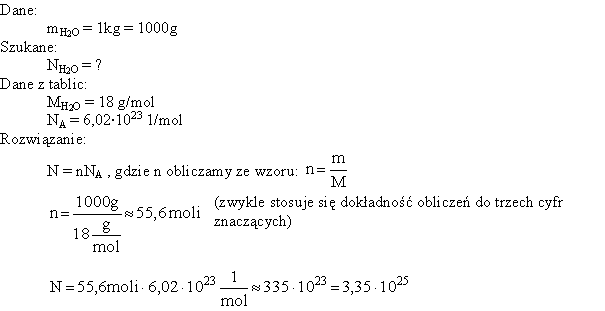
Warto sobie przy tym przypomnieć wzory działań na potęgach:
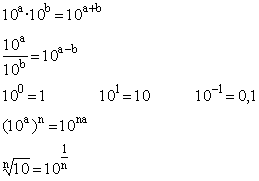
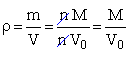
Kilka przykładów typowych zadań:
1A. Jaką masę posiada 1,12 dm3 tlenu w warunkach normalnych?
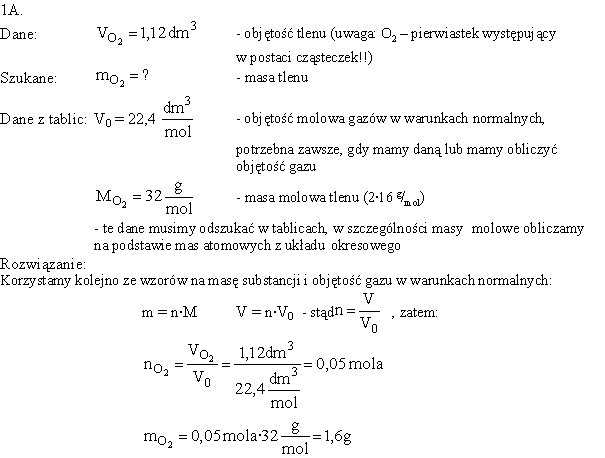

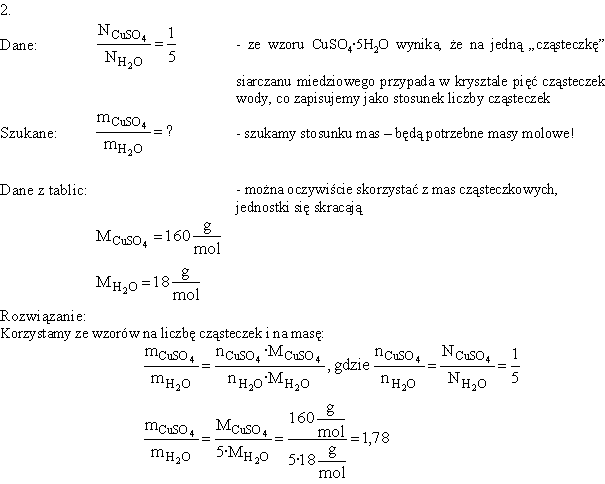

Do grupy zadań "molowych" zalicza się też czasem zadania polegające na obliczeniu wzoru związku chemicznego na podstawie składu ilościowego - zawartości procentowej lub stosunku masowego pierwiastków. Oto kilka przykładów:
4. Jaki wzór ma piryt (tzw. złoto głupców, minerał tworzący żółte, błyszczące kryształy), który zawiera żelazo i siarkę w stosunku masowym 7:8?

5. Określ wzór związku zawierającego 22,4% węgla, 2,8% wodoru i brom, jeżeli wiadomo, że masa cząsteczkowa tego związku wynosi 214 u. (Zadanie pochodzi ze zbioru: S. Hejwowska i in., Chemia organiczna, Zbiór zadań 2, Wydawnictwo Pedagogiczne Operon, Gdynia 2003)

6. Jaki wzór ma węglowodór, którego pary mają gęstość 39 względem wodoru?
Zadanie jest z pozoru beznadziejne - nie znamy zawartości pierwiastków, ani masy cząsteczkowej. Ale spójrzmy na to z drugiej strony - co jest wiadome. Po pierwsze, gęstość par względem wodoru, to "zaszyfrowana" informacja o masie cząsteczkowej. Ze wzoru na gęstość gazu wynika, że jest ona równa ilorazowi masy molowej i objętości molowej. Zatem stosunek gęstości dwóch gazów jest równy stosunkowi ich mas molowych. Z danych wiemy więc, że dany związek ma masę molową 39·2 = 78 g/mol.
Ponadto wiemy, że związek jest węglowodorem. Zawiera więc w cząsteczce n atomów węgla i, co najwyżej, 2n+2 atomów wodoru (ogólny wzór węglowodorów nasyconych to CnH2n+2). Stąd prosty wniosek, że masa cząsteczki złożonej z x atomów węgla (masa atomowa 12 u) oraz y atomów wodoru (masa atomowa 1 u), wynosi:
12x + y = 78, przy założeniu y ![]() 2x+1
2x+1
Ponieważ 78:12 = 6 R 6, zatem szukany wzór to C6H6 - najpewniej - benzen. Można sprawdzić, że dla x = 5 , y = 18 - nie spełnia warunków zadania.
Na zakończenie, małe zadanie domowe:
1. Oblicz, ile atomów żelaza jest zawartych w sześcianie o boku 1mm. Ile atomów przypada na jedną krawędź? (gęstość żelaza znajdziemy w tablicach)
2. Jaka jest różnica pomiędzy masą balonu w kształcie kuli o średnicy 10m i masie powłoki 100kg, wypełnionego helem, a masą powietrza wypartego przez ten balon? (średnia masa molowa powietrza równa się w przybliżeniu 29 g/mol)
3* Określ wzór związku pewnego pierwiastka z wodorem, jeżeli związek ten zawiera 12,5% wodoru. [Uwaga osobista od autora: Zadanie to pochodzi z jakiegoś starego zbioru zadań, nie pamiętam jakiego. Ja znalazłem jedno rozwiązanie, takie jak podane w odpowiedzi przez autora zbioru, natomiast moi, na wpół już legendarni uczniowie, Krzysztof C. i Aleksander Ś. znaleźli jeszcze dwa inne rozwiązania. Powodzenia!]
Uwaga
O ile w zadaniu nie jest podane inaczej, obliczenia przeprowadzamy dla warunków normalnych. Jeżeli zachodzi konieczność obliczeń dla innych warunków ciśnienia i temperatury, stosuje się równanie stanu gazu doskonałego, tzw. równanie Clapeyrona:

Literatura:
- Roman Mierzecki, Historyczny rozwój pojęć chemicznych, Państwowe Wydawnictwo Naukowe, Warszawa 1987;
- Krzysztof M. Pazdro, Prawo okresowości i struktura atomów, Wydawnictwa Szkolne i Pedagogiczne, Warszawa 1984